How To Import Template Haskell
This tutorial explores the Glasgow Haskell Compiler's compile-time meta programming in Template Haskell. Information technology motivates apply cases for meta programming and explains the different Template Haskell features on simple toy programs. The aim is to give an overview of Template Haskell'due south functionality in an case-driven fashion.
Contents
- one Introduction
- two Template Haskell by Examples
- 2.1 Template Haskell as a Code Generator
- 2.1.one Generic Maps
- 2.1.2 Reification
- two.2 Template Haskell for building Embedded Domain specific Languages (EDSLs)
- two.ii.i Shakespearean Templates
- 2.1 Template Haskell as a Code Generator
- 3 References
Introduction
Template Haskell (TH) is the standard framework for doing type-safe, compile-fourth dimension meta programming in the Glasgow Haskell Compiler (GHC). It allows writing Haskell meta programs, which are evaluated at compile-fourth dimension, and which produce Haskell programs as the results of their execution.
Template Haskell was conceived past Tim Sheard and Simon Peyton Jones[i] past drawing on the ideas of Lisp macros, but in the typed setting of Haskell. Since and so, the original implementation has evolved quite a flake[ii] [three]. Most notably, in 2007 Geoffrey Mainland added support for quasi quoting[4], which makes the embedding of domain specific languages into the Haskell host language much easier.
As it exists today, Template Haskell has two main areas of awarding: Haskell code generation at compile-fourth dimension and facilitating the embedding of domain specific languages.
As a code generator, Template Haskell empowers a user to write many, syntactically different, programs all at in one case by means of a single meta plan. All that is needed is a uniform, algorithmic clarification to create the dissimilar result programs. And the meta programme then precisely implements the algorithm to compute all the different result programs as its output. This proves useful for instance to avert writing the aforementioned repetitive, boilerplate code over and over again. To this terminate, Template Haskell is used (among many others) in the aeson library to automatically derive a data blazon'south ToJSON and FromJSON instances for JSON serialization; and in the lens library to mechanically create a data type's lenses.
Every bit a framework for creating domain specific languages (EDSLs), Template Haskell allows a user to embed programs written in another programming language inside of a Haskell program. This enables writing parts of the program in the concrete, domain specific syntax of a different programming language. It has the benefit to call up about -- and to limited -- domain specific problems in the language best suited for the task. In particular, it lets a user focus on the domain specific problem and removes all boosted linguistic communication burdens induced past inconvenient syntax, unsuited control constructs, etc. Programs from the embedded linguistic communication are parsed and translated into corresponding (only syntactically heavier) Haskell code at compile-time by Template Haskell. In this sense, (e.one thousand.,) the shakespearean template languages from the shakespeare library use Template Haskell at their cadre. They expose succinct domain specific languages to write HTML, CSS, and Javascript code inside of a Haskell based web awarding.
Template Haskell past Examples
In this section, we will review the Template Haskell features to write meta programs. The start set up of examples evidence-cases Template Haskell's potential as a lawmaking generator; the 2d set of examples highlights its facilities to create embedded domain specific languages (EDSLs). All examples require GHC's language extension TemplateHaskell to be enabled.
To avert confusion in the sequel, we distinguish between meta programs and object programs. Meta programs are the Haskell programs that run at compile-time and which generate Template Haskell object programs as the results of their execution; they are the programs that devise or dispense other programs by some algorithmic means. Object programs, on the other paw, are the Template Haskell programs manipulated and built by the Haskell meta programs at compile-time.
Template Haskell as a Lawmaking Generator
As an introductory example, consider Haskell's Prelude function curry :: (( a , b ) -> c ) -> a -> b -> c , which converts a function taking a pair to its curried equivalent. Unfortunately, there are no Prelude functions that provide the same currying functionality for functions taking arbitrary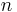 
-tuples. Moreover, having to write more than a few of these functions manually is, while trivial, a very repetitive and cumbersome task. Instead nosotros wish to generate needed curry3 , curry5 , or curry8 functions through a single meta program on demand. Template Haskell lets u.s.a. do just this. The thought is to write a meta function curryN :: Int -> Q Exp which, given a number n >= 1, constructs the source lawmaking for an 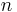-ary curry office:
{-# LANGUAGE TemplateHaskell #-} import Control.Monad import Language.Haskell.TH curryN :: Int -> Q Exp curryN n = do f <- newName "f" xs <- replicateM n ( newName "x" ) let args = map VarP ( f : xs ) ntup = TupE ( map VarE xs ) return $ LamE args ( AppE ( VarE f ) ntup ) For input 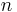, meta function curryN builds a lambda abstraction LamE that blueprint matches confronting a function f and 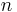argument variables x1 , x2 , ..., xn ; in its body, information technology and so applies function f to the 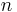-tuple ( x1 , x2 , ... , xn ) derived from the pattern matched variables. The names used to refer to the variables f and x1 through xn are generated monadically by part newName :: String -> Q Name to always generate fresh names non used anywhere else. Hence, the value returned by curryN is a monadic computation of type Q Exp. When executed, this monadic computation yields an expression Exp representing the object program of an 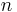-ary curry office. For example, ( curryN three ) returns a monadic ciphering that yields an expression representing a curry3 function of type (( a , b , c ) -> d ) -> a -> b -> c -> d in abstruse syntax.[5] [6]
To run a meta plan like curryN at compile-time, we enclose it with Template Haskell's splice operator $ past writing (e.g.,) $ ( curryN three ) . This evaluates the meta program curryN 3 and puts the resulting object program \ f x1 x2 x3 -> f ( x1 , x2 , x3 ) in identify of the splice. In general, the splice operator $ can be applied to whatever monadic Q ciphering, hereby performing this computation at compile-time and inserting the resulting object program every bit real Haskell code. To ensure type safe, meta programs to exist run are type checked beforehand to indeed yield a valid Template Haskell object program. Hence, just imported, fully-typechecked meta programs tin exist run via the splice operator $: in particular, we have to evaluate the meta program $(curryN 3) in a separate module to where curryN is defined.
To generate role declarations for the first 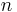curry functions, we can devise a further meta program on meridian of curryN as follows:
genCurries :: Int -> Q [ Dec ] genCurries north = forM [ ane .. due north ] mkCurryDec where mkCurryDec ith = do cury <- curryN ith permit name = mkName $ "curry" ++ show ith render $ FunD name [ Clause [] ( NormalB cury ) [] ] Running $ ( genCurries twenty ) will then splice in the kickoff 20 curry functions at compile-time, namely:
curry1 = \ f x1 -> f ( x1 ) curry2 = \ f x1 x2 -> f ( x1 , x2 ) curry3 = \ f x1 x2 x3 -> f ( x1 , x2 , x3 ) curry4 = \ f x1 x2 x3 x4 -> f ( x1 , x2 , x3 , x4 ) ... curry20 = \ f x1 x2 ... x20 -> f ( x1 , x2 , ... , x20 ) Notation that in this instance, genCurries returns a list of top-level part declarations that bind the anonymous lambda abstractions built by curryN . Also, to name the office bindings, nosotros utilize function mkName :: String -> Name instead of newName :: Cord -> Q Proper noun . The reason is that here nosotros want to generate functions curry1 to curry20 with exactly the prescribed names, so they can exist captured and referred to from other parts of the program.
Evaluating Haskell (meta) programs at compile-time and splicing in the generated object programs every bit regular Haskell code is the kickoff central edifice block of Template Haskell. The two other core mechanisms are exhibited past the implementations of curryN and genCurries : algebraic information types and the quotation monad Q.
First, object programs created by Template Haskell are represented every bit regular algebraic data types, describing a program in the form of an abstruse syntax tree. The Template Haskell library provides algebraic data types Exp, Pat, December, and Blazon to represent Haskell'due south surface syntax of expressions, patterns, declarations, and types, respectively. Nigh every physical Haskell syntactic construct has a corresponding abstract syntax constructor in one of the four ADTs. Furthermore, all Haskell identifiers are represented by the abstract Name data blazon. By representing object programs as regular algebraic data types (and thus equally data), normal Haskell tin exist used every bit the meta programming language to build object programs.
Second, Thursday object programs are built inside the quotation monad Q. This monad is performed past the splice operator "$" at compile-time as role of evaluating the meta program. In the examples and so far, the Q monad was merely needed to provide fresh identifiers with role newName :: Cord -> Q Name for the generated Haskell expressions. The other main characteristic that requires a monadic construction of object programs is reification, which allows to query compile-time data during the object program'south structure. We volition explicate reification in item later.
Thus, Template Haskell's core functionality constitutes evaluating object programs with "$" and building them from algebraic data types inside the quotation monad Q. Even so, constructing object programs in terms of their abstract syntax trees is quite verbose and leads to clumsy meta programs. Therefore the Template Haskell API likewise provides two farther interfaces to build object programs more conveniently: syntax structure functions and quotation brackets.
Syntax construction functions directly relate to the syntax constructors from the algebraic information types Exp, Pat, Dec, and Type for representing Haskell code. Even so, they hide the monadic nature of building object programs. For case, recall our definition of the genCurries meta function from higher up:
genCurries :: Int -> Q [ Dec ] genCurries northward = forM [ 1 .. north ] mkCurryDec where mkCurryDec ith = do cury <- curryN ith let name = mkName $ "back-scratch" ++ show ith return $ FunD name [ Clause [] ( NormalB cury ) [] ] To use the object program generated past the sub phone call to curryN in the larger context of the returned role annunciation, nosotros have to offset perform curryN and demark its result to cury . The reason is that we take to account for curryN 's generation of fresh names before we can proceed. Using syntax structure functions instead of data constructors, however, abstracts from the monadic construction of genCurries , thus making its code a fiddling shorter:
genCurries :: Int -> Q [ Dec ] genCurries n = forM [ 1 .. due north ] mkCurryDec where mkCurryDec ith = funD name [ clause [] ( normalB ( curryN ith )) [] ] where proper noun = mkName $ "curry" ++ show ith The new funD, clause, and normalB functions directly correspond to the formerly used FunD, Clause, and NormalB constructors. The but deviation lies in their types:
FunD :: Name -> [ Clause ] -> December | funD :: Proper name -> [ Q Clause ] -> Q Dec |
Clause :: [ Pat ] -> Body -> Clause | clause :: [ Q Pat ] -> Q Body -> Q Clause |
NormalB :: Exp -> Trunk | normalB :: Q Exp -> Q Trunk |
While the syntax constructors work with raw TH expressions, the syntax structure functions expect their monadic counterparts. They construct a Thursday object program straight in Q, thus freeing the API consumer from doing the monadic wrapping and unwrapping manually. For every syntax constructor, there is a respective monadic syntax construction function provided.
On meridian of syntax structure functions, quotation brackets are a further shortcut for representing Haskell code. They let to specify an object program using just regular Haskell syntax by enclosing information technology inside oxford brackets [| .. |]. That way, object programs tin exist specified yet much more than succinctly. For case, a meta programme building a Haskell expression for the identity function is still quite verbose, if expressed with either ADTs or syntax construction functions:
genId :: Q Exp genId = practise x <- newName "x" lamE [ varP x ] ( varE x ) Using quotation brackets, writing the aforementioned meta programme can be abbreviated much farther equally:
genId' :: Q Exp genId' = [ | \ 10 -> x | ] Quotation brackets quote regular Haskell lawmaking as the corresponding object program fragments inside the Q monad. In that location are quotation brackets for quoting Haskell expressions ([e| .. |]|), patterns ([p| .. |]), declarations ([d| .. |]), and types ([t| .. |]). Writing [| .. |] is hereby only another fashion of maxim [eastward| .. |]. Using quotation brackets in a sense lifts Haskell'south concrete syntax into corresponding object program expressions inside the Q monad. By doing so, quotation brackets represent the dual of the already introduced splice operator $: Evaluating a meta plan with "$" splices in the generated object programme as real Haskell code; in contrast, quotation brackets [| .. |] turn existent Haskell code into an object programme. Consequently, quotation brackets and the splice operator cancel each other out. The equation $([| due east |]) = due east holds for all expressions e and like equations concord for declarations, and types[two].
In addition, there is support for quoting Haskell (value and type) identifiers as respective Namedue south inside Template Haskell. This allows to refer to regular Haskell identifiers from inside Th object programs. For example, writing 'genId yields a Th Proper name referring to the genId identifier. Similarly, ''Q gives a Name referring to the Q type identifier.
Generic Maps
As a second instance that uses both syntax construction functions as well as quotation brackets, allow's consider a meta program mapN :: Int -> Q December to build "generic" map functions at compile-time. Invoking $ ( mapN 1 ) should generate the well-known standard function map :: ( a -> b ) -> [ a ] -> [ b ] ; evaluating $ ( mapN two ) should splice in a binary map function of blazon ( a -> b -> c ) -> [ a ] -> [ b ] -> [ c ] , and so on.[7]
mapN :: Int -> Q Dec mapN n | n >= 1 = funD name [ cl1 , cl2 ] | otherwise = neglect "mapN: statement n may not be <= 0." where name = mkName $ "map" ++ prove n cl1 = practice f <- newName "f" xs <- replicateM northward ( newName "x" ) ys <- replicateM n ( newName "ys" ) permit argPatts = varP f : consPatts consPatts = [ [ p | $ ( varP x ) : $ ( varP ys ) | ] | ( 10 , ys ) <- xs ` zip ` ys ] utilize = foldl ( \ chiliad x -> [ | $ g $ ( varE x ) | ]) start = utilise ( varE f ) xs balance = apply ( varE proper noun ) ( f : ys ) clause argPatts ( normalB [ | $ first : $ rest | ]) [] cl2 = clause ( replicate ( n + one ) wildP ) ( normalB ( conE ' [])) [] The implementation of mapN is very much in the spirit of meta function curryN from the first example. For instance, evaluating splice $ ( mapN three ) splices in the following map role at compile-time:
map3 f ( ten : xs ) ( y : ys ) ( z : zs ) = f x y z : map3 f xs ys zs map3 _ _ _ _ = [] Still, meta function mapN exhibits a couple of new Template Haskell features: Get-go, quotation brackets and splices are used in several places to abridge the object programme construction. For instance, helper definition utilise used to generate map3 's trunk f x y z : map3 f xs ys zs shows the use of quotation brackets; it as well highlights how splicing ( $ ) and quotes ( [ | .. | ] ) cancel each other out. 2d, identifier quotes (namely, ' [] ) are used to create an object program Name that refers to Haskell's built-in list constructor [] . Third, the example advertises how all iii APIs for building Template Haskell object programs tin can be interleaved. The lowermost verbose API of building a raw Th data value inside the quotation monad Q can be abbreviated, where possible, with syntax constructor functions and quotation brackets.
Lastly, the mapN example exemplifies how Haskell'south static scoping is extended to object programs. The scoping principle for object programs is just as in normal Haskell: Identifiers are jump to their lexically enclosing binders in telescopic at the point the object program is divers. Quotation brackets and splices don't alter static scopes, even though splices may bring an object programme into scope at a location, where a conflicting closure is present. For example, consider this snippet:
10 :: Int x = 42 static :: Q Exp static = [ | x | ] plus42 :: Int -> Int plus42 x = $ static + x Hither the occurrence of x in static refers to the global identifier ten that is lexically in scope during its definition. Splicing in static into a different scope later where a unlike local x is present (i.e., plus42 's local identifier x ), doesn't alter the link betwixt static 'southward ten and the global identifier ten .
The only exception to static scoping in Template Haskell are the names generated by mkName :: String -> Proper name . These names implement dynamic scoping and can exist captured in spliced-in code. Changing the previous snippet to
x :: Int ten = 42 dynamic :: Q Exp dynamic = VarE ( mkName "ten" ) times2 :: Int -> Int times2 ten = $ dynamic + x results in the identifier ten spliced in by $ dynamic to be jump to the closest x in scope. Hence, its binder is times2 's local identifier 10 and not the global 10 .
Reification
The last major Template Haskell feature not yet described is program reification. Briefly, reification allows a meta program to query compile-time information about other programme parts while constructing the object program. Information technology allows the meta programme to inspect other program pieces to answer questions such every bit: "what's this variable's blazon?", "what are the class instances of this type class?", or "which constructors does this data type have and and how practise they look like?". The chief use case is to generate boilerplate code which auto-completes manually written lawmaking. A prime example is to generically derive type class instances from blank data type definitions.
Suppose we've defined the following polymorphic information types for representing potentially erroneous values, lists, and binary trees, respectively:
information Consequence e a = Err e | Ok a information List a = Nil | Cons a ( List a ) data Tree a = Leaf a | Node ( Tree a ) a ( Tree a ) Moreover, suppose we desire to derive Functor instances for all of these types. Deriving these instances manually is straightforward, but writing them all out by hand is quite cumbersome. Particularly since writing a Functor instance follows the aforementioned pattern beyond all of the to a higher place types and in fact whatever type T a.
To brand a type constructor T an instance of Functor, 1 needs to implement method fmap :: ( a -> b ) -> T a -> T b . Its definition is hereby precisely adamant past parametricity and the functor laws: By parametricity, all values of type a must exist replaced according to the provided function with values of type b. Furthermore, by the functor laws, all other shapes of the input value of type T a must exist preserved when transforming it to the output value of type T b.
Meta function deriveFunctor :: Name -> Q [ December ] below implements the idea of this algorithm:
data Deriving = Deriving { tyCon :: Name , tyVar :: Name } deriveFunctor :: Name -> Q [ Dec ] deriveFunctor ty = do ( TyConI tyCon ) <- reify ty ( tyConName , tyVars , cs ) <- case tyCon of DataD _ nm tyVars cs _ -> return ( nm , tyVars , cs ) NewtypeD _ nm tyVars c _ -> render ( nm , tyVars , [ c ]) _ -> fail "deriveFunctor: tyCon may non be a type synonym." permit ( KindedTV tyVar Get-go ) = last tyVars instanceType = conT ''Functor ` appT ` ( foldl apply ( conT tyConName ) ( init tyVars )) putQ $ Deriving tyConName tyVar sequence [ instanceD ( return [] ) instanceType [ genFmap cs ]] where apply t ( PlainTV name ) = appT t ( varT name ) utilise t ( KindedTV name _ ) = appT t ( varT name ) Given the name of a type constructor (east.g. Outcome, List, etc.), deriveFunctor derives the code for this type constructor'southward Functor instance. For case, running the splice $ ( deriveFunctor ''Tree ) generates the post-obit code:
instance Functor Tree where fmap f ( Leaf x ) = Leaf ( f x ) fmap f ( Node l x r ) = Node ( fmap f l ) ( f x ) ( fmap f r ) Meta function deriveFunctor shows reification in action. It calls function reify :: Proper noun -> Q Info on the input type constructor's name to yield information nigh this information blazon's definition. Using reify , it thus learns whether the data type was defined using the data or newtype keyword, which constructors it defines and what their shapes are. Based on the learned structure, deriveFunctor is so able to generate a suitable definition of fmap and its different clauses via the auxiliaries genFmap , genFmapClause , and newField , defined below. These auxiliary definitions generate one fmap clause for each of the data type's constructors. And each clause and then transforms its constructor by recursively modifying all of the constructor's fields of type a through fmap 's function f, while retaining all other shapes.
genFmap :: [ Con ] -> Q December genFmap cs = do funD 'fmap ( map genFmapClause cs ) genFmapClause :: Con -> Q Clause genFmapClause c @ ( NormalC name fieldTypes ) = do f <- newName "f" fieldNames <- replicateM ( length fieldTypes ) ( newName "x" ) permit pats = varP f : [ conP name ( map varP fieldNames )] body = normalB $ appsE $ conE name : map ( newField f ) ( zip fieldNames fieldTypes ) clause pats body [] newField :: Name -> ( Name , StrictType ) -> Q Exp newField f ( x , ( _ , fieldType )) = practise Just ( Deriving typeCon typeVar ) <- getQ case fieldType of VarT typeVar' | typeVar' == typeVar -> [ | $ ( varE f ) $ ( varE ten ) | ] ty ` AppT ` VarT typeVar' | leftmost ty == ( ConT typeCon ) && typeVar' == typeVar -> [ | fmap $ ( varE f ) $ ( varE x ) | ] _ -> [ | $ ( varE 10 ) | ] leftmost :: Type -> Blazon leftmost ( AppT ty1 _ ) = leftmost ty1 leftmost ty = ty In more detail, deriveFunctor works as follows. First, via reify it observes the input data type's name tyConName , its declared blazon variables tyVars , and its exposed constructors cs . It then determines the data type'south right-most type variable tyVar and stores it together with the data type's type constructor proper name tyConName in the Q monad'south user land. This state information is retrieved later again from inside auxiliary definition newField . Next, deriveFunctor derives a Functor 'south fmap definition using auxiliary genFmap . For each of the input information type'southward value constructors cs , genFmap generates an fmap clause using helper office genFmapClause . The latter recursively maps the provided function f :: a -> b over all of a constructor'southward fields of blazon a, while leaving all other fields untouched. Each field is hereby modified through f or left unchanged by auxiliary newField based on the field'southward type: if a field'due south type is a (which is stored in the retrieved tyVar inside function newField ), then f needs to be applied to it; otherwise it needs to remain unchanged.
In an analogous manner to deriveFunctor , a part deriveFoldable :: Name -> Q [ December ] tin exist devised to derive a information blazon's Foldable instance. All that is needed is to provide a definition for function foldMap :: Monoid m => ( a -> m ) -> T a -> m . Again, foldMap 's definition follows direct from a information type's blank definition, which can exist observed past means of reification. This highlights particularly how the functionality offered by Template Haskell provides a low-level API into the GHC compiler to manipulate abstract syntax trees at compile-time. This mechanism is quite powerful and even allows to simulate some of GHC's offered language extensions, e.g., -XDeriveFunctor and -XDeriveFoldable, to be implemented as a library on superlative of Template Haskell.
Template Haskell for building Embedded Domain specific Languages (EDSLs)
To encounter Template Haskell'south potential for building an EDSL, consider the trouble of blueprint matching text with regular expressions. Suppose, as part of a Haskell plan nosotros need to devise many different regular expressions and use them to design match text fragments. Regular expressions are easily defined by an algebraic data type capturing their structure, as well as an evaluator checking whether a regular expression matches some input cord. [8]
data RegExp = Char ( Set Char ) -- [a], [abc], [a-z]; matches a unmarried graphic symbol from the specified class | Alt RegExp RegExp -- r1 | r2 (alternation); matches either r1 or r2 | Seq RegExp RegExp -- r1 r2 (concatenation); matches r1 followed by r2 | Star RegExp -- r* (Kleene star); matches r aught or more times | Empty -- matches only the empty cord | Void -- matches nada (ever fails) | Var String -- a variable property another regexp (explained afterward) deriving Show friction match :: RegExp -> String -> Bool match r southward = nullable ( foldl deriv r southward ) The evaluator friction match is hereby based on the concept of derivatives[ix]: an initial regular expression r matches an input string s , if r matches the first grapheme of due south and its derivative regular expression ( deriv r ) matches the residuum of southward :
nullable :: RegExp -> Bool nullable ( Char _ ) = False nullable ( Alt r1 r2 ) = nullable r1 || nullable r2 nullable ( Seq r1 r2 ) = nullable r1 && nullable r2 nullable ( Star _ ) = Truthful nullable Empty = True nullable Void = Faux nullable ( Var _ ) = False deriv :: RegExp -> Char -> RegExp deriv ( Char cs ) c | c ` Set . fellow member ` cs = Empty | otherwise = Void deriv ( Alt r1 r2 ) c = Alt ( deriv r1 c ) ( deriv r2 c ) deriv ( Seq r1 r2 ) c | nullable r1 = Alt ( Seq ( deriv r1 c ) r2 ) ( deriv r2 c ) | otherwise = Seq ( deriv r1 c ) r2 deriv ( Star r ) c = deriv ( Alt Empty ( Seq r ( Star r ))) c deriv Empty _ = Void deriv Void _ = Void deriv ( Var _ ) _ = Void The RegExp data type and the match function solve the initially posed problem of providing regular expressions in Haskell. However, specifying regular expressions in abstract syntax is extremely deadening. For example, consider defining a regular expression for checking the wellformedness of email addresses ending with the top level domain .com. In its usual concrete syntax, such a regular expression is easily defined every bit ([a-z]|[0-nine])*@([a-z]|[0-9])*.com, but writing information technology in terms of the RegExp dataype is verbose and unintuitive. Moreover, parsing functions like
-
compile :: String -> RegExp, or -
compile' :: String -> Either CompileError RegExp
practise not remedy the problem of working with regular expressions in physical syntax. Due to "compiling" regular expressions at run fourth dimension, they don't provide whatsoever compile-time type-rubber guarantees that the input raw expression is wellformed; thus they lead to either run time exceptions for illformed regular expressions (e.thou., compile ) or induce a tedious treatment for compiled regexes (east.g., compile' ).
To preserve type safety and yet to be able to use regular expressions conveniently, we want to embed the concrete regular expression syntax into the Haskell host language. This tin can be washed via Template Haskell'due south quasi quotes and furthermore enabling the QuasiQuotes extension. This allows defining quasi quotes for regular expressions, denoted [regex| .. |], where anything inside the quasi quote is considered office of an embedded regular expression language. Using quasi quotes, nosotros can so specify the regex for e-mail addresses from to a higher place naturally as follows:
{-# LANGUAGE QuasiQuotes #-} validDotComMail :: RegExp validDotComMail = [ regex | ([ a - z ] | [ 0 - 9 ]) *@ ([ a - z ] | [ 0 - 9 ]) *. com | ] We can fifty-fifty compose regular expressions easily from smaller building blocks:
alphaNum , validDotComMail' :: RegExp alphaNum = [ regex | [ a - z ] | [ 0 - 9 ] | ] validDotComMail' = [ regex |$ { alphaNum } *@$ { alphaNum } *. com | ] Writing $ { alphaNum } interpolates the regex referred to by alphaNum into the larger regex validDotComMail' . In essence, this means that we can ascertain our ain notion of splicing values from the Haskell meta language into the embedded object language of regular expressions. Nosotros can go further and even allow to run Haskell code when interpolating with ${..}. For example, refining our wellformedness check for .com mail service addresses, nosotros might want to ensure at least one character to occur on either side of the "@" symbol:
chars , validDotComMail'' :: RegExp chars = [ regex | [ a - z ] | [ A - Z ] | [ 0 - 9 ] | [ - _ . ] | ] validDotComMail'' = [ regex |$ { plus chars } @$ { plus chars } . com | ] plus :: RegExp -> RegExp plus r = Seq r ( Star r ) Here, plus corresponds to the usual regex combinator that requires a given regex to occur at to the lowest degree one time. Note how plus is defined every bit a regular Haskell function and and so used within of the embedded regex language to build the regular expression for validDotComMail'' .
Intuitively, a quasi quote like [regex| .. |] converts an embedded language's concrete syntax to Haskell code at compile-time. It is defined past a quasi quoter, which is a parser for the embedded language. Its task is to parse the embedded language'due south syntax into a corresponding Template Haskell expression then to splice this expression every bit real Haskell code in place of the quasi quote. The conversion of embedded language code to corresponding Haskell code hereby happens before typechecking the Haskell module. Hence, trying to splice in malformed embedded language fragments will raise a Haskell type error at compile-time.
The quasi quoter regex for our embedded language of regular expressions can be defined equally follows:
regex :: QuasiQuoter regex = QuasiQuoter { quoteExp = compile , quotePat = notHandled "patterns" , quoteType = notHandled "types" , quoteDec = notHandled "declarations" } where notHandled things = error $ things ++ " are not handled by the regex quasiquoter." compile :: String -> Q Exp compile s = case P . parse regexParser "" s of Left err -> fail ( bear witness err ) Right regexp -> [ e | regexp | ] That is, formally a QuasiQuoter consists of four parsers,
quoteExp :: Cord -> Q Exp quotePat :: Cord -> Q Pat quoteType :: String -> Q Blazon quoteDec :: String -> Q Dec to parse raw strings of the embedded language into the different categories of Haskell syntax. In this instance, nonetheless, nosotros simply want to splice embedded regular expressions into the context of Haskell expressions, so we only define the quoteExp parser in the regex quasi quoter. This parser compiles an embedded regular expression given as a string into a corresponding Template Haskell expression.
Compilation by the compile part proceeds in two stages: Kickoff, nosotros parse the input cord regex into a respective RegExp value. Second, we encode this RegExp value every bit a Haskell expression in Template Haskell's Q Exp blazon. It is the 2d footstep that allows usa to interpolate variables (or fifty-fifty code) from the Haskell host language into the EDSL for regular expressions.
Parsing a raw regular expression into a corresponding RegExp value is a routine chore using (e.chiliad.) the parsec library:
regexParser :: Parsec String () RegExp regexParser = alts <* eof where atom = try var <|> char var = Var <$> ( string "${" *> many1 ( noneOf "}" ) <* P . char '}' ) char = charclass <|> singlechar singlechar = ( Char . Set . singleton ) <$> noneOf specials charclass = fmap ( Char . Set . fromList ) $ P . char '[' *> content <* P . char ']' content = try ( concat <$> many1 range ) <|> many1 ( noneOf specials ) range = enumFromTo <$> ( noneOf specials <* P . char '-' ) <*> noneOf specials alts = effort ( Alt <$> seqs <*> ( P . char '|' *> alts )) <|> seqs seqs = attempt ( Seq <$> star <*> seqs ) <|> star star = try ( Star <$> ( atom <* P . char '*' )) <|> try ( Star <$> ( P . char '(' *> alts <* string ")*" )) <|> atom specials = "[]()*|" To stand for regular expressions of blazon RegExp as Template Haskell expressions of type Q Exp, Template Haskell's Lift typeclass is used. Its method elevator :: Lift a => a -> Q Exp lifts values from the Haskell meta linguistic communication (e.yard., a RegExp value) into Template Haskell's expression language (i.e., a Q Exp value). The elevator function is implicitly invoked by quote [ e | regexp | ] in function compile.
Most of the lifting is a straight encoding of the syntactic structure of the RegExp value; the only interesting case is when lifting the regular expression variable Var vars . In this example, nosotros treat the words in the cord vars as referring to identifiers from the Haskell host linguistic communication, which we apply in a left associative manner to each other. Doing this enables interpolation of Haskell identifiers or even simple forms of Haskell expressions into our EDSL of regular expressions equally shown by the regexes validDotComMail' , and validDotComMail'' to a higher place.
example Lift a => Lift ( Set a ) where elevator set = appE ( varE ' Set.fromList) (lift (Gear up.toList set)) instance Lift RegExp where -- lift :: RegExp -> Q Exp elevator ( Char cs ) = utilize ' Char [lift cs] lift ( Alt r1 r2 ) = apply ' Alt (map lift [r1, r2]) lift ( Seq r1 r2 ) = apply ' Seq (map lift [r1, r2]) lift ( Star r1 ) = apply ' Star (map lift [r1]) lift Empty = apply ' Empty [] lift Void = apply ' Void [] elevator ( Var vars ) = foldl1 appE $ map ( varE . mkName ) ( words vars ) utilize :: Name -> [ Q Exp ] -> Q Exp apply n = foldl appE ( conE north ) These two steps constitute the conversion of raw string regular expressions into Template Haskell expressions within of the compile function and define the regex quasiquoter. Whenever we write a quasi quote like [ regex | .. | ] in a Haskell expression context, regex 's parser quoteExp converts the regex EDSL into a Template Haskell expression Q Exp and splices in the result as a wellformed RegExp value. This example shows how Template Haskell and quasi quotes tin can be used to define a type-safety, domain specific language for regular expressions.
Shakespearean Templates
In much the same manner as in the last example, Template Haskell and quasi quotes are used in Michael Snoyman's shakespeare library[x] [11]. It defines embedded templating languages for working with the internet'southward web languages from within a Haskell web application. In detail, the shakespeare library provides the template languages Hamlet, Cassius, and Julius for writing embedded HTML, CSS, and Javascript lawmaking, respectively. All iii templating languages internally work quite similarly to the previous example's EDSL for regular expressions: quasi quotes let i to write HTML, CSS, or JavaScript code in concrete (though slightly modified) syntax inside of Haskell. Moreover, identifiers from the Haskell host language also as code fragments tin can be interpolated into the template languages at compile-time. In the residue we volition briefly show-case the shakespeare library'due south templating language Hamlet for creating HTML documents; the other templating languages Cassius and Julius are similar.
To create and output a simple spider web folio from inside a Haskell application, the following is enough:
import Data.Text import Text.Hamlet import Text.Bonfire.Html.Renderer.Cord data Folio = Home | Nigh | Github mkUrls :: Folio -> [( Text , Text )] -> Text mkUrls Abode _ = "/domicile.html" mkUrls Well-nigh _ = "/well-nigh.html" mkUrls Github _ = "https://www.github.com/bollmann" webPage :: Text -> Text -> HtmlUrl Page webPage title content = [ village | < html > < caput > < championship ># { Text . toUpper title } < body > < h1 ># { title } < div > Welcome to my Shakespearean Templates page ! < hr > < div > Links: < ul > < a href =@ { Home } > My Homepage < a href =@ { Most } > Well-nigh me < a href =@ { Github } > Check out my Github < hr > < div ># { content } | ] principal = putStrLn $ renderHtml $ webPage "Hello Shakespeare!" "Hello Globe!" mkUrls Running this Haskell programme, outputs an HTML page every bit specified past the Village templating language, embedded through quasi quote [ hamlet | .. | ] in role webPage . Hamlet closely resembles real HTML syntax, just is even more terse: instead of a endmost HTML tag, Hamlet uses indentation to indicate the span of the tag. Furthermore, Hamlet allows to interpolate code or identifiers from the Haskell host language when creating an HTML template. Interpolation of Haskell code into Hamlet is done by writing #{ .. }. In the above example, the HTML page'due south championship and content are interpolated from Haskell identifiers. Note particularly how in the webpage's title we capital the interpolated title using Haskell's Text . toUpper function inside of the Village language.
In addition to this standard interpolation, Hamlet can likewise interpolate links by writing @{..}. These links are specified as values of the Page information blazon within the template and the mkUrls render function translates them to real URLs later. Hamlet's URL interpolation is often described equally creating "type-safe URLs". Ane reason is that, merely similar with normal variable interpolation, all interpolated links have to exist and be type correct at compile-time; in this example, links must be values of the Page data type. Hence, equally soon as a link'south constructor shape is changed, the compiler statically forces usa to update all references to this link equally well. Furthermore, in that location is simply ane distinct place in the code to maintain or update a link's raw URL, thus minimizing the risk of dead URLs.
For case, suppose nosotros want to add more external links to our web page. We could model this fact past changing the Page data blazon to
information Folio = Home | Near | External ExternalPage data ExternalPage = Github | Haskell | Reddit and, moreover, changing the mkUrls renderer function to account for the new links:
mkUrls :: Folio -> [( Text , Text )] -> Text mkUrls Home _ = "/dwelling.html" mkUrls Nearly _ = "/nearly.html" mkUrls ( External page ) _ = mkExternalUrls page mkExternalUrls :: ExternalPage -> Text mkExternalUrls Github = "https://world wide web.github.com" mkExternalUrls Haskell = "http://www.haskell.org" mkExternalUrls Reddit = "http://www.reddit.com/r/haskell" Doing just these changes, will then crusade a compile-fourth dimension error in our webPage template, since nosotros haven't updated the Github reference to our newly adjusted link structure. Hence, the compiler reminds (and in fact forces) usa to update all locations in the code that used the onetime Github link to now use the new External Github (likewise as optionally the External Haskell , etc.) links.
Finally, Hamlet allows to use some command constructs like if-conditionals, for-loops, and permit-bindings to embed basic business logic into a webpage'south template. Michael Snoyman gives a gentle (and much more in-depth) introduction to shakespearean templates and Yesod[10] [12].
References
- ↑ Tim Sheard and Simon Peyton Jones. Template Meta-Programming for Haskell. SIGPLAN Non., 37(12):60-75, Dec 2002. URL: https://world wide web.microsoft.com/en-united states of america/research/publication/template-meta-programming-for-haskell/?from=http://enquiry.microsoft.com/~simonpj/papers/meta-haskell/
- ↑ 2.0 2.one Tim Sheard and Simon Peyton Jones. Notes on Template Haskell, Version 2. URL: https://www.haskell.org/ghc/docs/papers/th2.ps, 2003.
- ↑ Simon Peyton Jones. Major Proposed Revision of Template Haskell. URL: https://ghc.haskell.org/trac/ghc/blog/Template%20Haskell%20Proposal, 2010
- ↑ Geoffrey Mainland. Why it'south nice to be quoted: Quasiquoting for Haskell. In Proceedings of the ACM SIGPLAN Workshop on Haskell, Haskell '07, pages 73-82, New York, NY, U.s., 2007. ACM
- ↑ Note that meta function
curryNcannot be written in normal Haskell per se as the type for a generated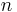-ary curry function depends on 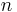. Thus, the definition of curryNrequires dependent types to be expressed in Haskell, a feature not nonetheless present. All the same, in that location already exist ingenious alternatives to "faking" dependent types in Haskell; see for case this newspaper for a solution to simulate functions likecurryNwithout dependent types). - ↑ Daniel Friedlender and Mia Indrika. Do nosotros need Dependent Types? J. Funct. Program. 10(4):409-415, July 2000.
- ↑ Note that 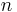-ary maps are better written using Applicative Functors and
ZipLists, as this allows to define them kickoff-grade from inside regular Haskell. For understanding Template Haskell equally a code generator, this example is still useful though. - ↑ This case draws on Penn'southward CIS 552 Advanced Programming class, specifically Consignment 5: http://www.seas.upenn.edu/~cis552/current/hw/hw05/Main.html.
- ↑ Janusz A. Brzozowski. Derivatives of regular expressions. J. ACM, 11(iv):481–494, October 1964.
- ↑ 10.0 10.i Michael Snoyman. Shakespearean Templates. URL: http://world wide web.yesodweb.com/book/shakespearean-templates [Accessed: May 2016].
- ↑ Michael Snoyman. The
shakespeareHaskell library. URL: http://hackage.haskell.org/package/shakespeare [Accessed: May 2016]. - ↑ Michael Snoyman. Haskell and Yesod. URL: http://www.yesodweb.com/book-one.iv [Accessed: May 2016].
How To Import Template Haskell,
Source: https://wiki.haskell.org/A_practical_Template_Haskell_Tutorial
Posted by: longgonly1982.blogspot.com
0 Response to "How To Import Template Haskell"
Post a Comment